The solution of a system of linear equations is a list of value(s) for the variable(s) that
make all of the equations in the system true. Since every point on the graph of an
equation solves that equation, the solution of a system of linear equations will be the
intersection of the graphs of the equations. One of the methods for solving linear
equations is using differences. In this lesson you will learn about the difference of two
equations and how to use this difference to find their point of intersection.
Finding differences between graphs
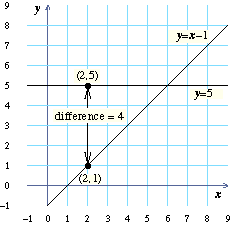
Look at the diagram below or the grid to the left. The
point $(2,1)$ is on the line $y=x-1$.
The point $(2,5)$ is on the line $y=5$.
To find the difference between the
two lines when $x=2$, we can find the difference between the
$y$-coordinates of these points. So, the difference is:
$5-1=\cl"red"4$.
|
What is the difference between the lines $y=5$ and
$y=x-1$ when $x$ is 1?
| |
|
Which line is above the other when $x$ is 1?
| |
|
Which line is above the other when $x$ is 7?
| |
When $x$ is 8, the lines $y=5$ and
$y=x-1$ are 2 units apart. At the differences we computed
in the previous question, the line $y=5$
was above the line $y=x-1$. To show that now
$y=x-1$ is above $y=5$, we use a negative
sign. So when $x$ is 8, the difference between $y=5$ and
$y=x-1$ is $-2$.
Complete the table below. To complete the “difference” column, find the difference between
the graphs of $y=5$ and $y=x-1$ on the grid
to the left.
| $x$ | $y=5$ | $y=x-1$
| difference
$d$
|
|---|
|
As you get closer to the point of intersection, does the difference get closer
to zero or further from zero?
| |
|
What is the difference between the two lines at the point of intersection?
| |
|
The red points on the grid to the left have coordinates
$(x,d)$ from your table above.
What shape is formed by these red points (circle, line,
triangle, …)?
| |
You can find the equation for the line that goes through the
red points by finding the
difference between the two original equations. So, the equation for the line is:
$$
\cl"tight"{\table
d,=,5,-,(x-1);,=,5,-,x+1;,=,\colspan 3 {6-x}
}$$
Let’s find the point of intersection of the lines $y=2x+1$ and
$y=x-2$. First we will find the equation for $d$. To find $d$,
we need to find the difference between the two equations:
$$\cl"ma-join-align"{\table d,=2x+1-(x-2); ,=2x+1-x+2; ,=x+3}$$
|
What is the $x$-coordinate of the $x$-intercept of $d=x+3$?
(You can find the $x$-intercept of the equation by plugging in 0 for $d$.)
| |
|
What is the $x$-coordinate of the point of intersection of $y=2x+1$
and $y=x-2$? (Remember, this is where their difference, $d$, is 0.)
| |
|
Plug the $x$-coordinate of the point of intersection into
$y=x-2$ to find the $y$-coordinate of the point of intersection.
| |
|
What is the point of intersection of the lines $y=2x+1$ and $y=x-2$?
| |
Here are the graphs of the equations
$y=2x+1$,
$y=x-2$ and
$d=x+3$ from solveQn.
Click or tap inside the grid and drag to the left or right.
To the right of the grid you will see the $y$ and
$d$ values for each $x$ value you choose. For example,
when you move the bar to $x=4$, you will see $y=9$, $y=2$, and $d=7$.
This means that, when $x$ is 4:
- $y=9$ in the first equation,
- $y=2$ in the second equation, and
- $d$, the difference between the lines, is 7.
|
Use the graph to find the point of intersection of the two lines
$y=2x+1$ and
$y=x-2$
(the blue lines).
| |
|
Does this answer match the answer to the last part of solveQn?
| |
Complete the table below. Check your answers to make sure
that the point of intersection you found satisfies both equations.
To fill in the second column, subtract the two equations as shown in
solveQn.
To get the values in the third column, plug $d=0$ into the
equation in the second column.
To get the values in the fourth column, plug the value from the third column into either
of the two original equations.
| equations
| difference
$d$
| $x$-value of
point of
intersection
| $y$-value of
point of
intersection
| Point of
intersection
|
|---|
|
In the last example above, is there a point of intersection? (Is $d$
ever 0?)
| |
|
In that example, are the two lines parallel?
| |
Lines in standard form
Up until now, we’ve been solving systems of equations in
slope-intercept form ($y=mx+b$). You can also use this method to solve
systems of equations in standard form ($Ax+By=C$) by first converting
those equations into slope-intercept form.
Convert the equation $4x+2y=6$ from standard form into slope-intercept form.