Equations for Lines in Standard Form

On the grid to the left you can see the graph of $4x+2y=4$. What shape is the graph of $4x+2y=4$ (triangle, circle, line, square, …)?

The slope of a line is a measurement of how steep it is. Use the figures below to help remind you about how to measure the slope of a line. The first line graphed below has slope $$3/2$$, while the second one has slope $$-3/2$$.

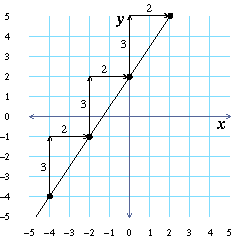
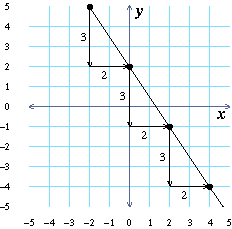
Look at the grid to the left to answer the following questions.

What is the slope of $4x+2y=4$?

What is the $y$-intercept of $4x+2y=4$ (where does it cross the $y$-axis)?

What is the $x$-intercept of $4x+2y=4$ (where does it cross the $x$-axis)?

The effects of A, B, and C

To the left is the graph of $Ax+By=C$. You are looking at the graph of $4x+2y=4$ (because $A=4$, $B=2$, $C=4$). Use the sliders to change the values of $A$, $B$, and $C$ and notice how each affects the shape and position of the graph of $Ax+By=C$.

Each row of the following table has a question about how the graph changes when you change $A$, $B$, or $C$. Answer the question for each of the three variables.

	When $A$ changes	When $B$ changes	When $C$ changes
Does the graph of the equation remain a line?
Does the $x$-intercept of the graph change?
Does the $y$-intercept of the graph change?
Does the slope of the graph change?

The form $Ax+By=C$, where $A$, $B$, and $C$ are constants, is called the standard form for an equation for a line.

Use the sliders to set $A=4$, $B=2$, and $C=4$. You are again looking at the graph of $4x+2y=4$. Slide the value of $A$ toward zero.

Look at what happens to the slope of the graph as $A$ gets closer and closer to zero. Does the graph become steeper or less steep?

What is the slope of the graph when $A=0$?

Set $A$ back to 4. Now, slide the value of $B$ toward zero and look at what happens to the slope of the graph as $B$ gets smaller. Does the graph become steeper or less steep?

Each row of the table below gives an equation for a line in standard form. Using the sliders, change the values of $A$, $B$, and $C$, and complete this table. In each case, find the slope of the line by looking at the grid to the left.

$Ax+By=C$	$A$	$B$	slope

Using the pattern in the table, what do you think the slope of $2x+5y=40$ is?

The slopes you have found suggest that:

The slope of the line $Ax+By=C$ is $$-A/B$$.

Converting from standard form to slope-intercept form

In the last question, you found the slopes of lines by looking at their graphs. If you want to find the slope of a line algebraically, by using its equation, you can convert that equation into slope-intercept form.

For example, we can write the equation $4x+2y=4$ in slope-intercept form as follows:

$$ \cl"tight ma-join-align"{\table \text"Standard form:  ", , 4x+, 2y, =, , 4; \text"Subtract" \: 4x \: \text"from both sides:  ", -4x+, 4x+, 2y, =, -4x+, 4; , , , 2y, =, -4x+, 4; \text"Multiply both sides by" \: 1/2 \text":  ", , , 1/2(2y), =, \colspan 2{1/2(-4x+4)}; \text"Distribute:  ", , , y, =, 1/2(-4x)+, 1/2(4); \text"Slope-intercept form:  ", , , y, =, -2x+, 2 } $$

Each row of the table has an equation in standard form. Write that equation in slope-intercept form.

The equations from convertQn have been summarized in the table below. Use them to answer the following questions.

	Equation in standard form	Equation in slope-intercept form
	$4x+2y=4$	$y=-2x+2$

Is it possible for two different equations in standard form to give you the same line?

What is the slope of the line whose equation is $8x+2y=6$? (Use the slope-intercept form of that equation.)

What is the $y$-intercept of the line whose equation is $6x+3y=6$?

Finding the $x$- and $y$- intercepts of a line in standard form

The $y$-intercept of a line is the point on that line where $x=0$, and the $x$-intercept is the point where $y=0$. You can use this to find the intercepts of lines algebraically.

Algebraically find the $y$-intercept of each line in the table below.

	equation for the line	set $x=0$	$y$-intercept

Algebraically find the $x$-intercept of each line in the table below.

	equation for the line	set $y=0$	$x$-intercept

Finding an equation for a line in standard form

By using the sliders to change the values of $A$, $B$, and $C$, find an equation (in standard form) for the line with $x$-intercept $(2,0)$ and slope 3. (Try setting $C$ to 6.)

For the equation you just found, find the slope using the formula $$m=-A/B$$.

$A=$ $B=$ $m=$

By using the sliders to change the values of $A$, $B$, and $C$, find an equation (in standard form) for the line with $x$-intercept $(-2,0)$ and $y$-intercept $(0,1)$.

Look at the line you just graphed. What is its slope?

Now, compute the slope of this line using the formula $$m=-A/B$$. (Should this answer be the same as your previous answer?)

$A=$ $B=$ $m=$